Yield Locus Analysis | Mercury Scientific Inc

The yield locus analysis is designed to determine the angle of internal friction and cohesion for a sample material and then calculate its overall strength under compressive load.This is achieved by measuring the failure strength of a sample under various loads after consolidation under a preset pre-shear load. Plotting the failure strength of the material under different loads generates a yield locus for the sample under the pre-shear load.

The test consists of three parts for every point on the yield locus: consolidation, steady state and failure analysis. Depending on the type of cell used, failure points can be generated on the same sample or fresh sample can be used for each failure point. Generally 3 to 5 points are used to generate the yield locus due to the time required for each point as well as the wear on the sample. If time consolidation is used, a delay time occurs after the steady state step.

In the consolidation step, the sample in the measurement cell is compressed to the preset normal load.With linear cells, this step includes twisting of the lid to help pack the material in the cell to what is called its “critical consolidation”.Critical consolidation is defined as the sample density at which it will reach a steady shear with minimal shear travel.This state in indicated by constant sample density or by a leveling off of the drop in normal load after each twist of the cell lid.For rotational cells, the consolidation step simply consists of compressing the sample until the normal load is reached.

Sample Consolidation

Normal Load versus Time

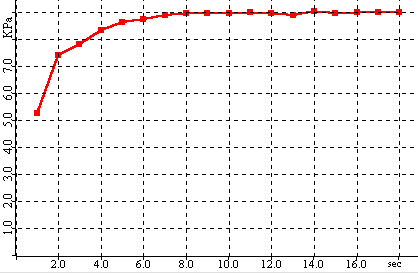
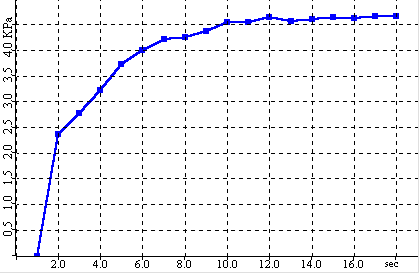
In the steady state step, shear stress is applied to the sample until the measured shear force and sample volume become stable. With linear cells, the shear stress is applied by moving pushing the lower ring of the cell at a fixed rate relative to the upper ring.For rotational cells, the lid is rotated a fixed rate. The steady state point is the point at which the shear force becomes stable.At the steady state point, the sample has reached a repeatable, stable density relative to the applied compressive load.

Steady State

Shear Force versus Time

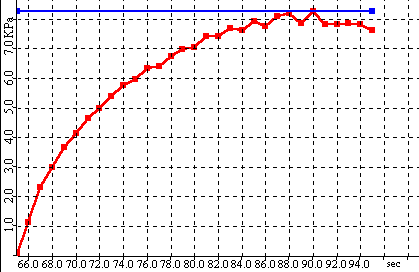
In the analysis step, the shear stress is reduced to zero by reversing the shear stress mechanism.The normal load is then reduced to a predetermined level called the shear load and the shear stress is again applied.The shear forces rises as the sample resists shearing until a maximum shear force is reached.At this point the sample fails and the shear force drops rapidly.The generate yield point consists of the maximum shear force and the shear load.

Static Failure Analysis

Shear Force versus Time

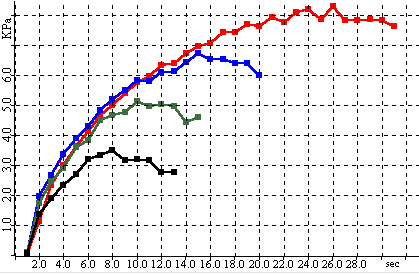
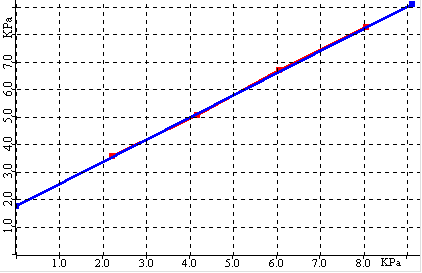
By repeating the above sequence 3 to 5 times, a series of yield points are generated from which a yield locus can be plotted.The yield points are selected so that they are in the linear portion of the yield locus.

Static Failure Points

Shear Force versus Time

A least squares regression is performed to calculate a linear function for the yield locus.The slope of the calculated line is the angle of internal friction.The intercept of the line is the cohesion.From the cohesion, angle of internal friction and steady state point, the unconfined yield strength and major consolidation stress are calculated using Mohr Coulomb equations.

Static Yield Locus

Shear Force versus Normal Load

Because the yield points are generated by measuring several steady states for the same sample, the steady state point used for the strength calculation is the average of all the steady state points.In addition, to account for the effect of the steady state on the measured shear force during failure analysis, the measured shear force can be adjusted based on whether its steady state was higher or lower than the average.This is called prorating and can correct for variations in sample density for each yield point measurement.

Compressibility is calculated using the sample’s initial density and density after the consolidation step.

Static yield analysis generates the strength of a static or not-moving sample.This would be the condition in a silo or chute when the sample is at rest.Therefore, to get the sample to flow, the force used to move the sample must be greater than the static yield strength.